LeetCode——最小路径和

NO.64 最小路径和中等

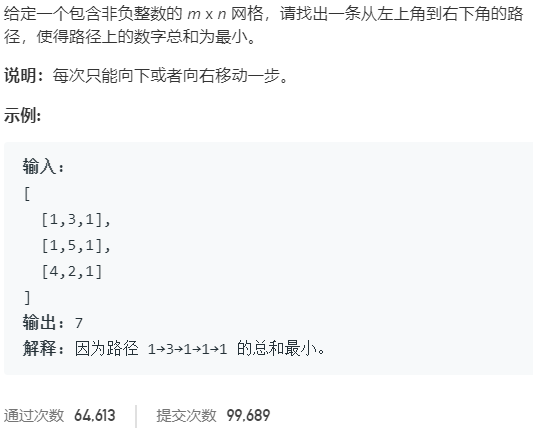
思路一：动态规划 我们要找最小路径和，一定是走数值较小的位置并且不往回走不绕路，又因为是从左上走到右下，所以每次都向右或者向下移动。

dp数组的含义：dp[i][j]走到[i][j]位置的最小路径和。

初始化：dp[0][0]=[0][0]

状态转移：dp[i][j]=Min(dp[i-1][j]+dp[i][j-1])+[i][j]，因为每次只能向右或向下移动，所以[i][j]选择上方[i-1][j]或者左方[i][j-1]较小的路径走过来加上当前位置本身的值。要注意第一行没有上方、第一列没有左方。

public int minPathSum(int[][] grid) {
    int row = grid.length,col=grid[0].length;
    int[][] dp=new int[row][col];
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            //第一行
            if (i==0&&j!=0)dp[i][j]=dp[i][j-1]+grid[i][j];
            //第一列
            else if (j==0&&i!=0)dp[i][j]=dp[i-1][j]+grid[i][j];
            //中间部分
            else if (j!=0&&i!=0)dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+grid[i][j];
            //第一个元素[0][0]
            else dp[i][j]=grid[i][j];
        }
    }
    return dp[row-1][col-1];
}

时间复杂度：O(rowcol) 空间复杂度：O(row\col)

优化空间复杂度 直接在grid数组自身每个位置记录对应的最小路径和。

public int minPathSum(int[][] grid) {
    int row = grid.length,col=grid[0].length;
    for (int i = 0; i < row; i++) {
        for (int j = 0; j < col; j++) {
            //第一行
            if (i==0&&j!=0)grid[i][j]=grid[i][j-1]+grid[i][j];
            //第一列
            else if (j==0&&i!=0)grid[i][j]=grid[i-1][j]+grid[i][j];
            //中间部分
            else if (j!=0&&i!=0)grid[i][j]=Math.min(grid[i-1][j],grid[i][j-1])+grid[i][j];
            //第一个元素[0][0]
            else grid[i][j]=grid[i][j];
        }
    }
    return grid[row-1][col-1];
}

时间复杂度：O(row*col) 空间复杂度：O(1)

本人菜鸟，有错误请告知，感激不尽！

更多题解和学习记录博客:博客、github

NO.64 最小路径和 中等

NO.64 最小路径和中等